Harbor seal vibrissa morphology inspires comprehensive computational simulations and experiments studying footprints left behind moving hydrodynamic objects for online database

 

By Sarah Dulac

 

Portrait of Sarah Dulac

 

My OUR project was rewarded with a grant this summer 2020, from the Office of Undergraduate Research (OUR) to conduct research via Remote desktop due to the recent pandemic under supervision of Dr. Banafsheh Seyed-Aghazadeh. My OUR research project was entitled ‘Harbor seal vibrissa morphology inspires comprehensive computational simulations and experiments studying footprints left behind moving hydrodynamic objects for online database’.

The objective of the research is to experimentally and computationally quantify the left behind footprint from different hydrodynamic objects at varying velocities, to help better understand how the harbor seal’s whisker reacts to these stimuli like a sensor. Using both the experimental and computational data collected, another goal was to create an online platform that would provide valuable data to numerous other research projects and educational purposes to anyone looking to learn. This was a fully remote project and some of my tasks are yet to be completed due to my limited access to the needed campus facilities. This project depended heavily on self-reliance, which allowed me to gain new skills including literature review to Computational Fluid Dynamics.

In order to understand how the harbor seal whisker detects the hydrodynamic pattern from a fast-starting fish, investigating the flow response of stationary cylinders with different cross-sections is principal. The information about possible flow characteristics of a left behind footprint is not available in literature, which is a crucial step to better understand the mechanism behind this “sensing”. The first step towards better understanding of these footprints left behind, is to investigate the flow response of the cylinders with different cross-sectional geometries using Computational Fluid Dynamics (CFD). Flow past a circular cylinder is the foundational start to a path for studying more complex shaped bodies and their footprint’s produced. The case of flow past a circular cylinder has a great deal of attention in research due to its simplicity of flow results and it is a very common phenomenon in engineering applications.

Starting with building and running computational simulations on COMSOL Multiphysics simulation software was a challenge considering my first step was to learn how to use the fluid flow module before successfully modeling my application. I found numerous resources online that allowed to me build my knowledge on how to correctly model my simulation. In order to verify my simulation is running correctly, data including RMS lift C_L, mean drag coefficient C_D, and Strouhal number St were gathered and analyzed to verify quantitatively.

Where L, D, ρ, U, A, ƒ, and d are lift force, drag force, density, inflow velocity, area, frequency of vortex shedding, and diameter, respectively. A computational model was constructed using the laminar flow module under fluid flow on COMSOL Multiphysics. The governing equations are the incompressible Navier-Stokes equation(1) which represents the conservation of momentum and the continuity equation(2) which represents the conservation of mass.

The domain was computed using laminar flow model in COMSOL Multiphysics because of the flow being in the range of Reynolds number equal to 100, characterizing the flow as laminar. Reynolds number is a dimensionless quantity that predicts whether the flow of a fluid on a surface is laminar or turbulent.

Where, ρ, U, d and μ are density, inflow velocity, diameter and dynamic viscosity, respectively. The domain and the constructed mesh is shown in Figure 1. Experiment[4] and simulations[1,2,3] of flow past a circular cylinder were used to compare my results. Simulations[5,6,7] of flow past a square cylinder were used to compare my results. Experiment[9] and simulation[8] of flow past a triangular cylinder were used to compare my results. Results of mean drag coefficient for circular, square and triangular cylinders are all plotted in Figure 2. Results of RMS lift for circular and square cylinders are all plotted in Figure 3. Results for the triangular cylinder were not plotted in this figure due to the reference literature using mean lift coefficient alternatively, which resulted in a value of zero because of the symmetry of the geometry. Strouhal numbers were also plotted for all cylinders as shown in Figure 4. From comparison of my resulting values and what is found in literature, I was able to confirm my simulation was running correctly.

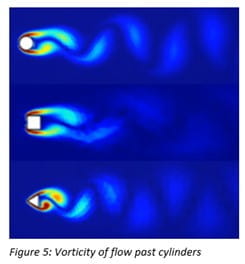
Along with gathering and analyzing RMS lift, mean drag coefficient and Strouhal number qualitative methods of visualizations were used as well. The post processing tools offered on COMSOL Multiphysics have allowed me to plot the vorticity of the flow past the cylinders as shown in Figure 5. A tutorial of how to set up the CFD simulations and post process important data will be created to serve as an educational tool for MNE 332 – Fluid Mechanics and for an online library with open access.

There was one other task I was able to complete due to the needs of the task being accessed remotely. This task consisted of designing and constructing a three dimensional (3D) model of the whisker geometry using solid modeling computer-aided design program (SOLIDWORKS), which was available through UMassD remote access. The final design of the whisker has been completely modeled using SOLIDWORKS (Figure 6) and it ready to be 3D printed. For my future with this project, it consists of experimentally investigating the flow response of stationary cylinders with different cross-sections including the whisker geometry designed. The data gathered from all CFD simulations and experiments will be organized in a way, so it is easy to navigate and access via the online library.

Sources

[1] Park, J., Kwon, K., & Choi, H. (1998). Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160. KSME International Journal, 12(6), 1200-1205. doi:10.1007/bf02942594

[2] Singha, S., & Sinhamahapatra, K. (2010). Flow past a circular cylinder between parallel walls at low Reynolds numbers. Ocean Engineering, 37(8-9), 757-769. doi:10.1016/j.oceaneng.2010.02.012

[3] Tezduyar, T., Mittal, S., Ray, S., & Shih, R. (1992). Incompressible flow computations with stabilized bilinear and linear equal-order-interpolation velocity-pressure elements. Computer Methods in Applied Mechanics and Engineering, 95(2), 221-242. doi:10.1016/0045-7825(92)90141-6

[4] Tritton, D. J. (1959). Experiments on the flow past a circular cylinder at low Reynolds numbers. Journal of Fluid Mechanics, 6(4), 547-567. doi:10.1017/s0022112059000829

[5] Sohankar A, Norberg C, Davidson L. Low-Reynolds-number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition. International Journal for Numerical Methods in Fluids 1998; 26:39–56.

[6] Sahu AK, Chhabra RP, Eswaran V. Two-dimensional unsteady laminar flow of a power law fluid across a square cylinder. Journal of Non-Newtonian Fluid Mechanics 2009; 160:157–167.

[7] Singh AP, De AK, Carpenter VK, Eswaran V, Muralidhar K. Flow past a transversely oscillating square cylinder in free stream at low Reynolds numbers. International Journal for Numerical Methods in Fluids 2009; 61:658–682.

[8] Bao, Y., Zhou, D., & Zhao, Y. (2009). A two-step Taylor-characteristic-based Galerkin method for incompressible flows and its application to flow over triangular cylinder with different incidence angles. International Journal for Numerical Methods in Fluids. doi:10.1002/fld.2054

[9] Seyed-Aghazadeh, B., Carlson, D. W., & Modarres-Sadeghi, Y. (2017). Vortex-induced vibration and galloping of prisms with triangular cross-sections. Journal of Fluid Mechanics, 817, 590-618. doi:10.1017/jfm.2017.119